



With a highly customizable study planner tool, Live Review Sessions 6 days/week at no extra charge, plus practice tests, hundreds of on-demand video explanations, you can truly tailor your MCAT preparation.
Blueprint MCAT teaches you how the MCAT thinks. Our exams & interface are the most representative, after the AAMC, so you will be extra prepared and confident on test day.
Our Self-Paced Course was created by 524+ scoring instructors & more than 50 of our tutors have scored 520+ on the MCAT. Meet our MCAT instructors and tutors.
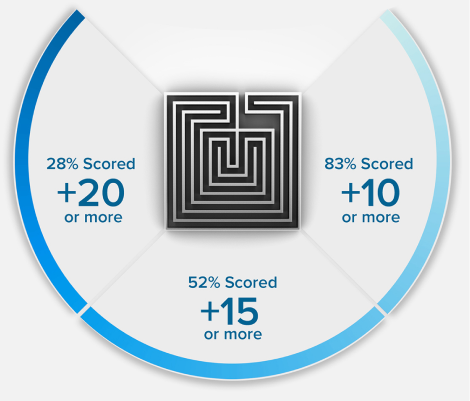
Because we’re so confident in our methodology, we guarantee that your MCAT exam score will increase or your money back. Recent results showed future medical students increased their MCAT score by an average of 15 points.
Check out how Blueprint courses
helped future medical students like you achieve their MCAT score goals
15 POINTS? WE DON'T STOP THERE.
+15
POINTS ON AVERAGE*

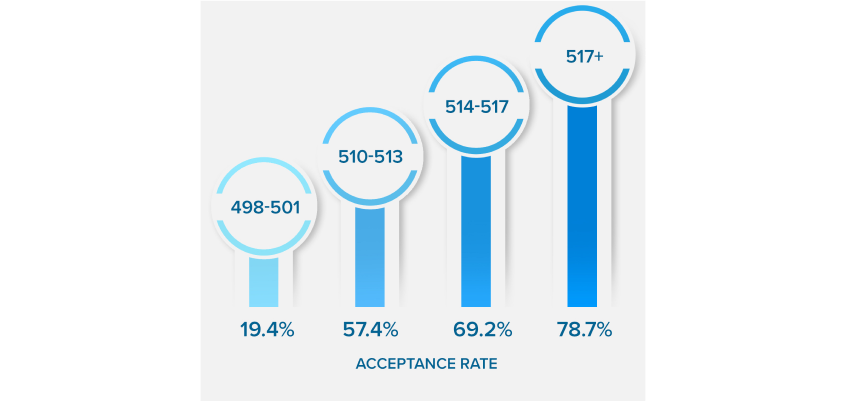

NEARLY QUADRUPLE
YOUR ACCEPTANCE RATE
*Results based on our Live Online MCAT Course Cohort. See more details on score increases.
You will be taken to another Blueprint Prep company site or one of our partners. Do you want to continue?
Request a consultation with an MCAT Advisor, or call 888-530-6398 for immediate assistance.